Volume d'un absorbeur acoustique
Absorption, optimum, minimum, volume, phase
Jean Boulvert
8/10/20257 min lire
Cet article de blog analyse la compacité des traitements acoustiques absorbants passifs à partir de la théorie de la réflexion à phase minimale.
Retrouvez ICI des outils d'analyse et de minimisation du volume des absorbeurs.
Les éléments théoriques sont issus de l'article de Yang Meng, Hao Dong, Eric Ballestero, Simon Félix, Gwénaël Gabard, et Jean-Philippe Groby du Laboratoire d’Acoustique de l’Université du Mans, UMR CNRS 6613, France, publié dans Physical Review Applied en décembre 2024 et intitulé Minimum-phase reflection for a passive acoustic absorber with target absorption spectrum and minimum volume. DOI: 10.1103/PhysRevApplied.22.064074
Introduction
Les informations et les outils présentés ici sont valides lorsque le traitement acoustique considéré est passif (résonateurs de Helmholtz, quart d'onde, plaques perforées, matériaux poreux, leurs assemblages et leurs variantes repliées), monté en fond rigide (pas de transmission), et soumis à une onde en incidence normale, sans écoulement d'air, et dans son régime linéaire.
L'utilisation de ces outils peut être utile pour répondre aux problématiques suivantes :
Analyse d'un traitement acoustique existant
La même absorption que celle apportée par le traitement acoustique pourrait-elle être obtenue avec un traitement de volume plus faible ?Comparaison de traitements acoustiques absorbants
Comment comparer la performance d'absorption de traitements acoustiques présentés dans la littérature ou par des fabricants s'ils n'ont pas été optimisés vis-à-vis du même objectif (épaisseurs différentes, plages de fréquences d'intérêt différentes...) ?Optimisation d'un traitement acoustique
Grâce à quelle fonction coût peut-on maximiser son absorption et minimiser son volume ?
Le même coefficient d'absorption peut être obtenu par des traitements différents
Le même coefficient d'absorption peut être obtenu par des traitements différents. La différence entre les traitements peut venir de la typologie de résonateurs qui les composent (résonateurs de Helmholtz VS matériaux poreux, etc) ou bien simplement de leur volume.
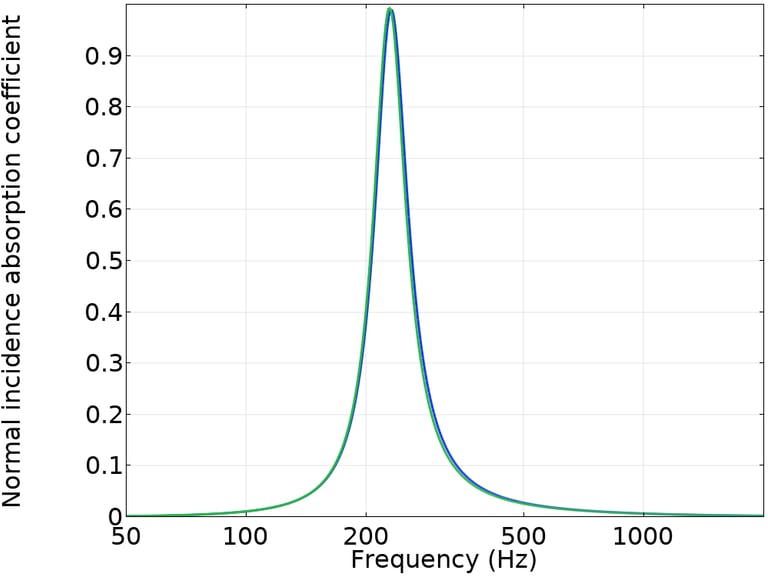
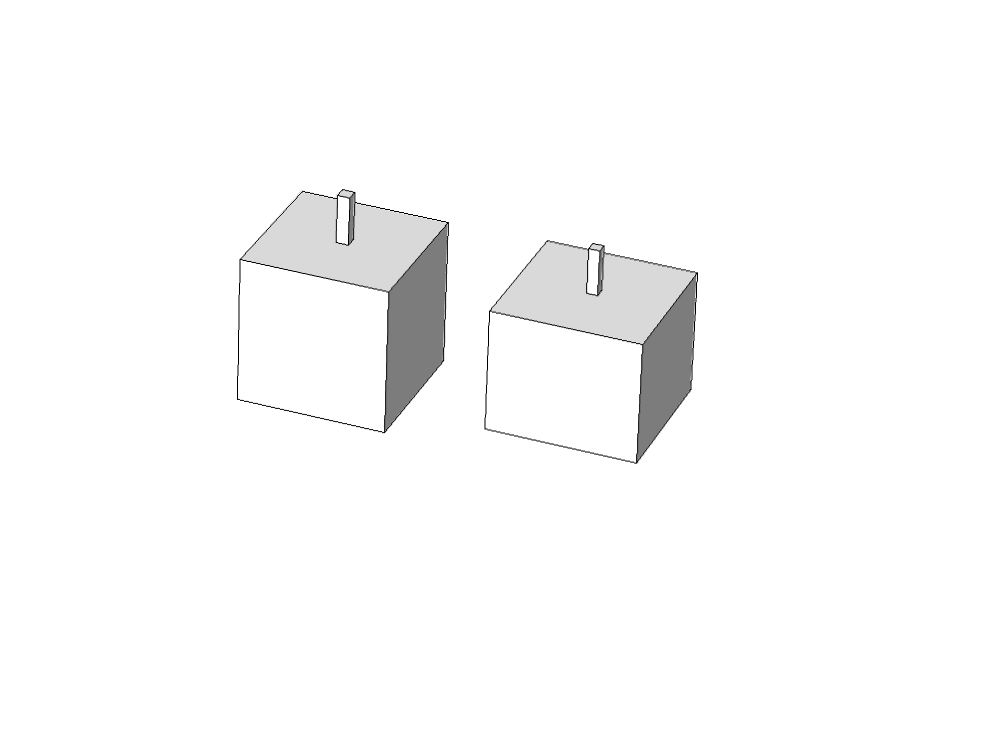
Par exemple, les résonateurs de Helmholtz présentés ci-dessous offrent des coefficients d'absorption en incidence normale très similaires (calcul via Comsol Multiphysics, courbes bleu et verte presque superposées) bien qu'ayant un rapport de volume de 1,2. Des rapports de volume de 2 peuvent être atteints et donc beaucoup d'espace perdu !
Lorsqu'un traitement fait appel à N résonances, il existe jusqu'à 2^N conceptions différentes donnant lieu au même coefficient d'absorption.
Volume minimum
Le volume théorique minimum d'air qui doit constituer un traitement acoustique pour présenter le coefficient d'absorption α est, Eq. 1 :
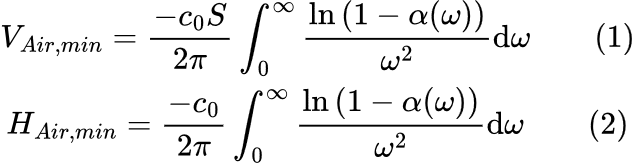
Avec
c₀, la vitesse du son dans l'air
S, l'aire de la surface soumise à l'onde incidente
α, le coefficient d'absorption en incidence normale
ω, la pulsation (ω = 2 π f)
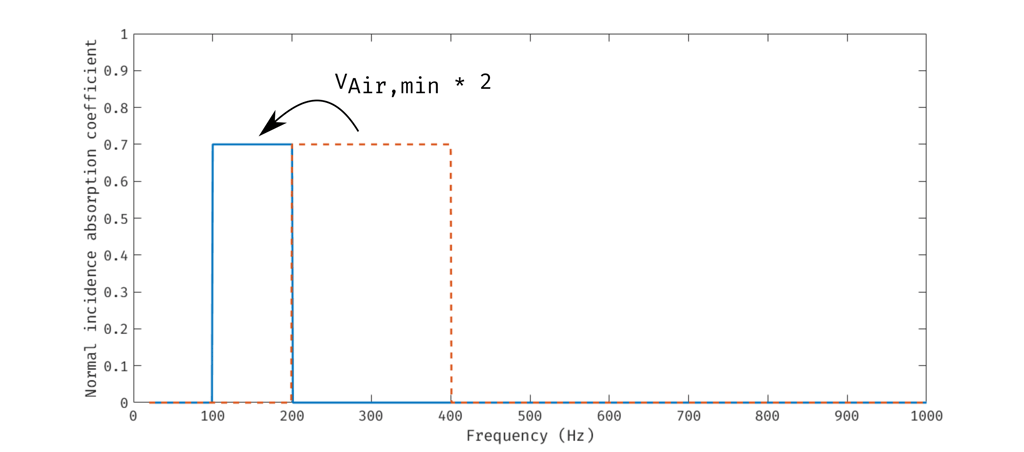
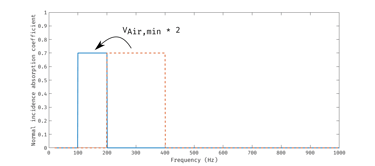
La présence du ω² au dénominateur de l'intégrande illustre que plus la fréquence est basse et plus une absorption élevée demande un traitement volumineux. Le coefficient d'absorption bleu ci-dessous demande un volume minimum 2 fois plus important que le coefficient d'absorption orange pointillés.



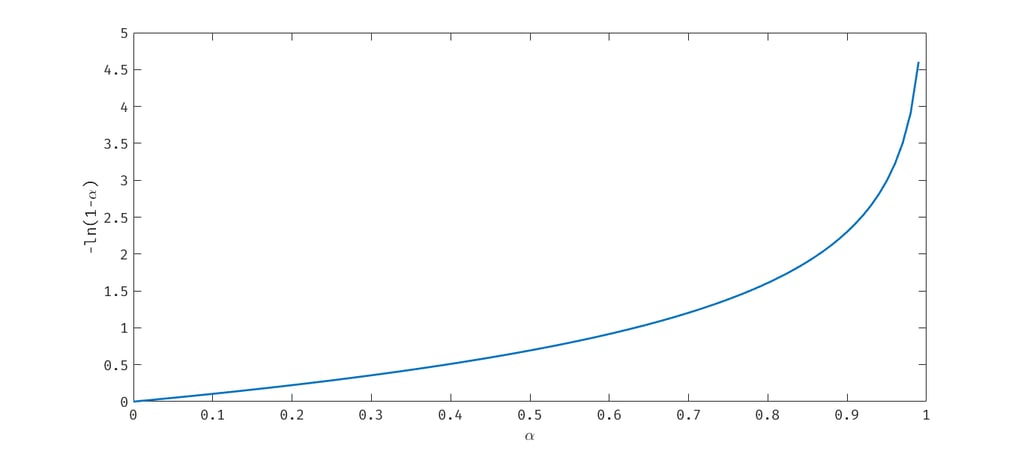
La présence du coefficient d'absorption au sein du logarithme népérien au numérateur de l'intégrande illustre que l'absorption et le volume minimum ne sont pas linéairement liés. De plus, cette formule implique que le coefficient d'absorption soit strictement inférieur à 1.
La courbe ci-dessous illustre -ln(1-α) = f(α).
En fonction de l'application visée (ex : TR de salle, perte par insertion d'un encoffrement), tracer la valeur d'intérêt en fonction de -ln(1-α) permet de raisonner en fonction du volume nécessaire au traitement et non pas seulement en fonction de son absorption.
Hauteur minimale
Dans la plupart des cas, la surface du traitement soumise à l'onde incidente est identique à la surface de la face supérieure du traitement. C'est par exemple le cas lorsqu'un matériau est à l'intérieur d'un tube d'impédance ou qu'il est constitué d'une cellule unitaire répétée périodiquement en latéral. Dans ce cas, la hauteur d'air minimale du traitement est donnée par l'Eq. 2 :
Géométrie des 2 résonateurs de Helmholtz
Champ de pression à 200 Hz
Coefficient d'absorption des 2 résonateurs
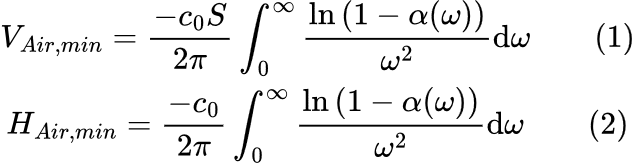
Dans le cas où les deux surfaces sont différentes, par exemple si un échantillon dépasse latéralement d'un tube d'impédance, alors il faut multiplier le terme de droite de l'égalité par S/Str où Str est l'aire de la face supérieure du traitement.
C. Évaluation de la concentration de l'absorption sur la plage de fréquence voulue
Les traitements étudiés dans la littérature sont souvent optimisés de sorte à maximiser leur absorption sur une plage de fréquences [fmin ; fmax] et variable d'un article à l'autre. Il en résulte que les traitements optimisés présentent un plateau d'absorption sur la plage de fréquences d'intérêt.
Il est possible d'évaluer leur performance en se focalisant uniquement sur l'absorption comprise entre fmin et fmax. En effet, vu qu'il s'agit de la plage de fréquence utilisée lors de l'optimisation, il est raisonnable de considérer que seule cette partie du spectre est d'intérêt applicatif.
Cette évaluation porte sur la concentration de l'absorption sur la plage de fréquences d'intérêts. Autrement dit, la meilleure évaluation est obtenue lorsque l'absorption est un échelon borné par fmin et fmax.
L'indice de performance (P2) est défini comme la hauteur théorique d'air nécessaire pour donner lieu à l'absorption du traitement sur [fmin ; fmax] rapportée à la hauteur théorique d'air nécessaire pour donner lieu à l'absorption complète du traitement :
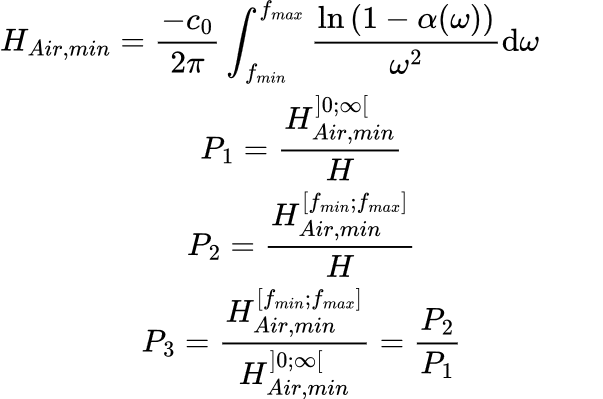
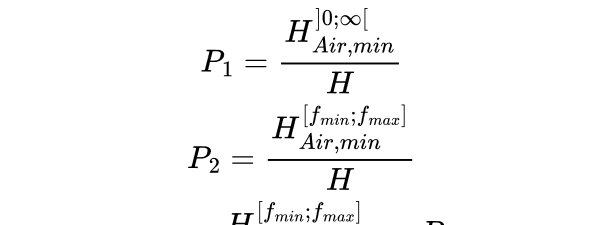
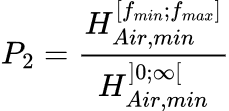
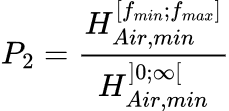
Analyse de la performance d'un traitement acoustique
Lorsqu'un (méta)matériau est étudié, développé, optimisé, il est souvent question de performance acoustique et d'évaluation de la performance : tel matériau est-il meilleur qu'un autre ? La question sous-jacente est double :
La typologie du traitement (types et agencement des résonances) est-elle intrinsèquement plus favorable qu'une autre pour bien absorber le son ?
L'optimisation a-t-elle été efficace, c'est-à-dire, a-t-elle maximisé l'absorption tout en minimisant le volume du traitement ?
A. Évaluation de la performance applicative brute
L'évaluation consiste à comparer l'absorption du traitement à une absorption cible : absorption moyenne sur une ou une autre plage de fréquences, indice unique issus d'une norme, etc.
Il est alors indispensable de comparer entre eux uniquement des traitements optimisés vis-à-vis du même objectif et d'épaisseur égale. Il est attendu qu'un traitement optimisé de sorte à maximiser son absorption sur la plage [2000 ; 8000] Hz ait une absorption moyenne sur la plage [500 ; 2000] Hz plus faible qu'un autre traitement optimisé sur [500 ; 2000] Hz. Cela n'est pas dû à la typologie des traitements ou la qualité de leur optimisation, mais à la différence d'objectif.
Un indice de performance basé sur une telle comparaison est forcément arbitraire car non basée sur un optimum théorique ou une norme étalon.
Pour définir les indices de performance suivants, il est nécessaire de définir une nouvelle grandeur généralisant l'Eq. 2. Il s'agit de la hauteur d'air théorique minimale pour atteindre un coefficient d'absorption donné sur la plage de fréquences [a ; b]. Autrement dit, le coefficient d'absorption est considéré comme nul en dehors de [a ; b] :
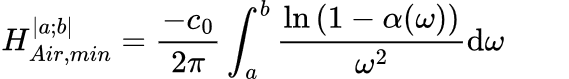
B. Évaluation de la bonne exploitation du volume
L'évaluation consiste à comparer le volume (resp. la hauteur) d'air théorique minimum donnant lieu à l'absorption du traitement avec le volume (resp. la hauteur) du traitement.
Cette évaluation se concentre uniquement sur la bonne exploitation du volume, qu'importe que le coefficient d'absorption ait un fort potentiel applicatif ou non. Il s'agit d'une mesure des volumes "perdus" : parois solides (dont on ne peut pas se passer complètement), et surtout, qualité de l'optimisation. En effet, comme présenté plus haut, la même absorption peut être obtenue avec des traitements de volume différents.
L'indice de performance (P1) est ainsi défini comme la hauteur théorique d'air nécessaire pour donner lieu à l'absorption du traitement rapportée à la hauteur du traitement :
Exemple
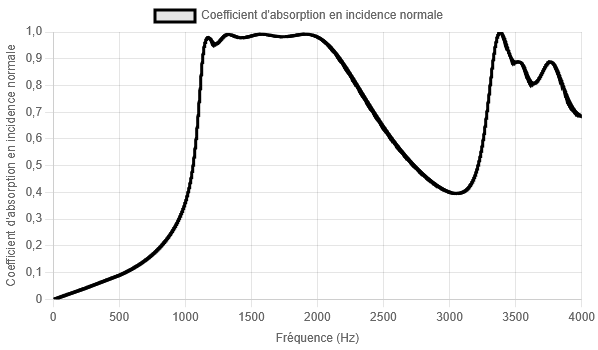
Un traitement d'épaisseur H = 3 cm présente une absorption supérieure à 0.95 sur la plage [1150 ; 2100] Hz. En dessous et au-dessus de cette plage de fréquences, son absorption décroit rapidement et n'a donc pas d'intérêt applicatif. Il a été optimisé de sorte à maximiser son absorption sur [1150 ; 2000] Hz.
La description classique de la performance du traitement est :
Absorption sub-longueur d'onde : λₒ(1150 Hz) / H = 9.9...
... sur 0.9 octave = log2(2100/1150).
... et quasi-parfaite > 0.95.
Les indices proposés valent :
(P1) = 0.79 ➝ Le volume du traitement est bien exploité, peu d'espaces sont perdus par des parois structurelles ou des résonateurs inutilement volumineux. ➝ Cette typologie de traitement permet de bien valoriser l'utilisation de l'espace pour générer de l'absorption.
(P2) [1150 ; 2000] Hz = 0.55 ➝ L'absorption est moyennement concentrée dans la plage de fréquences d'intérêt. En effet, l'absorption décroit relativement lentement avant et après (moins problématique) le plateau.