Acoustic panels in shoe soles

Fashion clothing isn't really my thing 😅

But when I saw my brother-in-law's Adidas shoes, I couldn't help thinking they could be used to make acoustic panels!

Some shoe soles are made using 3D printing. The soles then form an open-porosity material. This means that, a priori, they can absorb airborne noise. So why not reclaim the soles of these end-of-life shoes for DIY acoustic treatment?

Behind the lightness of the subject, it's an opportunity to showcase Sil&Add's expertise in numerical simulation, notably via COMSOL Multiphysics, of the acoustic behavior of porous materials.

DIY Acoustic Panels, V. 1.0: Egg Boxes

Egg cartons are sometimes reused to make DIY acoustic panels.

This makes it possible to obtain acoustic panels from reused packaging, and thus limit environmental impact.

However, egg cartons are generally flammable, and the aesthetic appeal of an acoustic panel made from egg cartons is not universally appreciated!

And acoustically?

Egg cartons can't soundproof a wall. In other words, placing egg cartons on the wall of a bedroom or music studio will not contain the noise inside the room.

They do, however, absorb noise, and can offer an NRC of up to 0.7.

As detailed in the article linked opposite, absorption is highly dependent on the egg-crate model used and its orientation.

DIY acoustic panels, V. 4.0 : Printed soles

These Adidas shoe soles are industrially produced using the “Digital Light Synthesis” 3D printing process. They are composed of a 3D lattice of polymer material designed to offer a better walking and running experience. In fact, the material of the sole transfers part of the vertical force to the horizontal and thus helps to move forward. What's more, the geometry of the cells features a gradient that allows local control of the material's stiffness.

These soles are a fine example of the application of theoretical research in materials mechanics and additive processes!

To find out more about the history of these soles and their manufacture, here's a fascinating report from which the illustrations opposite are taken:

And acoustically?

The material used for these insoles is primarily designed for its mechanical properties.

However, the 3D mesh forms a material with millimetric open porosities, making it ideal for noise absorption.

To better understand the material's acoustic potential, we can use numerical simulation to analyze its intrinsic acoustic behavior and then use this to predict its overall behavior.

A. Intrinsic acoustic behavior

The intrinsic acoustic behavior of a material derives from its micro-geometry: the size and shape of its pores. This material can be modeled acoustically as a fluid. To do this, we use the Johnson-Champoux-Allard-Larfarge (JCAL) model, which describes equivalent fluids by six parameters: porosity, tortuosity, viscous characteristic length, thermal characteristic length, visco-static permeability and thermo-static permeability.

The parameters of the JCAL model can be obtained by two main families of methods:

• Inverse characterization. A sample of the material is characterized experimentally (e.g., by obtaining the reflection and/or transmission coefficient from an impedance tube), then an algorithm is used to derive the JCAL parameters from the measurement results.

• Numerical prediction. A numerical reproduction of the material, often reduced to a very small unit cell, is performed. Numerical calculations are then used to obtain the JCAL parameters (e.g. two-scale asymptotic homogenization method).

Here, we use a numerical method.

From a photograph of the material, a rough digital 3D reproduction is produced. For projects requiring greater rigor, much more precise reproduction methods can be employed (e.g. 3D scan, tomography). The equivalent fluid parameters (porosity, tortuosity, etc.) are then calculated using Comsol Multiphysics.

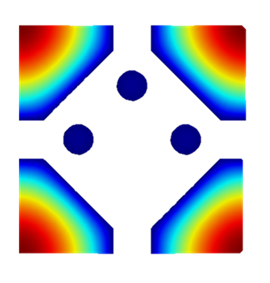
B. Overall acoustic behavior

The overall acoustic behavior of a material is its response to an acoustic field, once the material has been shaped. This behavior therefore depends on the material (its intrinsic behavior), its thickness, its arrangement with other materials... and the acoustic field: angle(s) of incidence, sound level (important if very high)...

Here, we consider a flat, homogeneous 2.5 cm-thick panel made of the material presented above, subjected to a diffuse field and resting on a rigid wall. Once again, this is a rough pre-study of the use of footings to form acoustic panels. It is possible to refine the modeling by taking into account a more complex geometry.

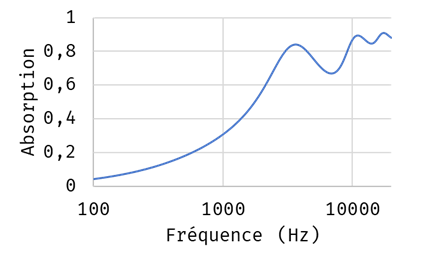
The calculation is carried out analytically and the diffuse field absorption coefficient is shown in the figure below.

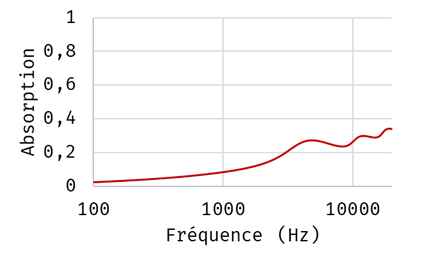
The sound absorption of the shoe-sole panel studied is low. At the same time, it's not what you'd expect from a shoe sole.

C. Modifying the material to make it absorbent

Not all porous materials with open pores are good absorbers. In the case of a homogeneous material, the rule of thumb is that the pore size must be of the same order of magnitude as the viscous sub-layer for the material to absorb well. In addition, it is preferable for the porosity to be high (>80%) so that the absorption coefficient as a function of frequency does not show strong oscillations. 

Shoe sole material therefore has pores too large to be a good absorber of airborne noise.

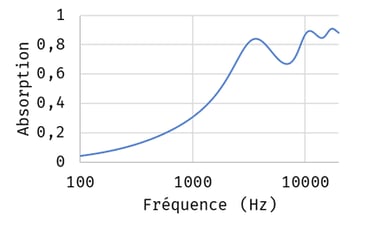
Let's imagine that the same unit cell is used, but that it is 10 times smaller, as shown in the image opposite.

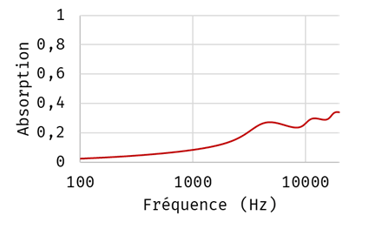
The absorption of the flat, homogeneous 2.5 cm thick panel would then have the diffuse-field absorption coefficient shown in the figure below. Absorption is much higher than with the original material!

Unit cell size and geometry can be optimized to maximize the acoustic performance of whatever material is being shaped. Not very useful for shoe soles, this can be very relevant in other applications where mechanical and acoustic properties need to be optimized simultaneously.