Volume of an acoustic absorbing panel

This blog article analyzes the compactness of passive absorbing acoustic treatments based on the theory of minimum-phase reflection.

The theoretical foundations are drawn from the article by Yang Meng, Hao Dong, Eric Ballestero, Simon Félix, Gwénaël Gabard, and Jean-Philippe Groby from the Laboratoire d’Acoustique de l’Université du Mans, UMR CNRS 6613, France, published in Physical Review Applied in December 2024 and entitled Minimum-phase reflection for a passive acoustic absorber with target absorption spectrum and minimum volume. DOI: 10.1103/PhysRevApplied.22.064074

Find HERE tools for analyzing and minimizing absorber volume.

Introduction

The information and tools presented here are valid when the considered acoustic treatment is passive (Helmholtz resonators, quarter-wave resonators, perforated plates, porous materials, their assemblies, and folded variants), mounted on a rigid backing (no transmission), and subjected to a normally incident wave, without airflow, and in its linear regime.

The use of these tools can be helpful to address the following issues:

• Analysis of an existing acoustic treatment
  Could the same absorption provided by the treatment be achieved with a smaller-volume solution?

• Comparison of absorbing acoustic treatments
  How can the absorption performance of treatments presented in the literature or by manufacturers be compared if they have not been optimized with respect to the same objective (different thicknesses, different frequency ranges of interest, etc.)?

• Optimization of an acoustic treatment
  With which cost function can one maximize absorption while minimizing volume?

The same absorption coefficient can be obtained with different treatments

The same absorption coefficient can be achieved using different treatments. The differences between treatments may stem from the type of resonators that compose them (Helmholtz resonators vs. porous materials, etc.) or simply from their volume.

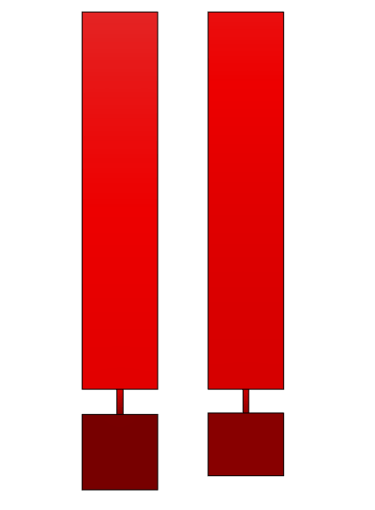
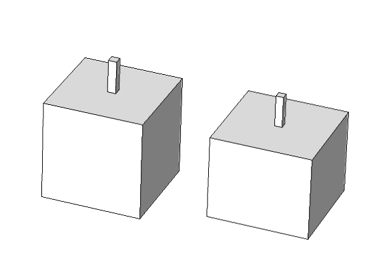
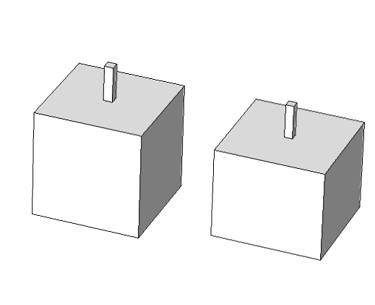
For example, the Helmholtz resonators shown below provide very similar normal-incidence absorption coefficients (calculated using Comsol Multiphysics, with the blue and green curves almost overlapping), despite having a volume ratio of 1.2. Volume ratios of 2 can be reached, which means a significant amount of wasted space!

When a treatment relies on N resonances, there can be up to 2^N different designs leading to the same absorption coefficient.

Minimum volume

The theoretical minimum volume of air required for an acoustic treatment to achieve the absorption coefficient α is given by Eq. 1:

with

c₀, the speed of sound in air
S, the cross-sectional area of the treatment
α, the normal-incidence absorption coefficient
ω, the angular frequency (ω = 2πf)

The presence of ω² in the denominator of the integrand illustrates that the lower the frequency, the larger the volume required to achieve high absorption. The blue absorption coefficient shown below requires a minimum volume twice as large as the dotted orange absorption coefficient.

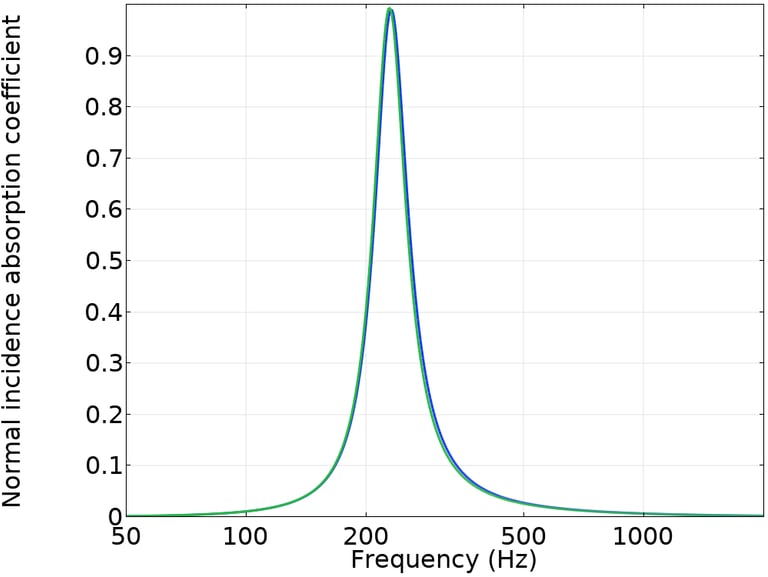
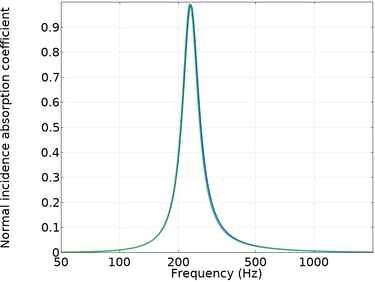
The presence of the absorption coefficient inside the natural logarithm in the numerator of the integrand shows that absorption and minimum volume are not linearly related. Moreover, this formula implies that the absorption coefficient must be strictly less than 1.

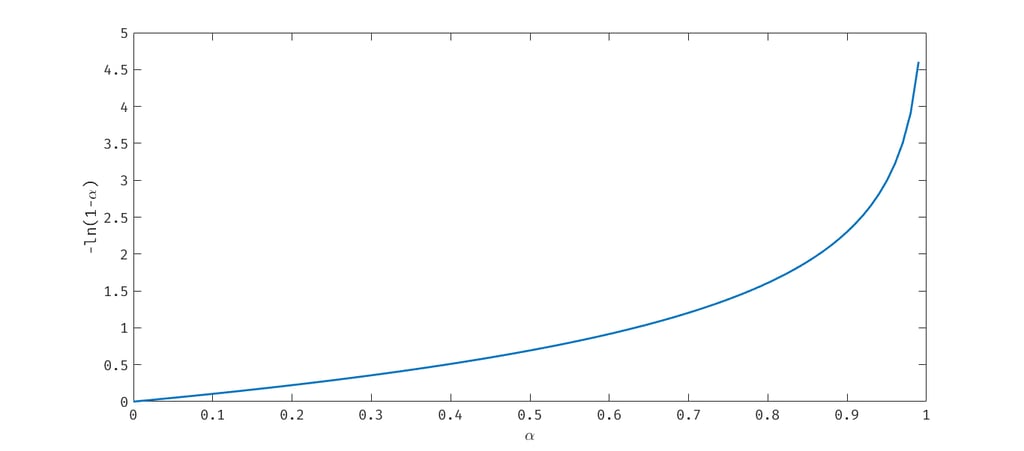
The curve below illustrates −ln(1−α) = f(α).

Depending on the intended application (e.g., room reverberation time, insertion loss of an enclosure), plotting the value of interest as a function of −ln(1−α) makes it possible to reason in terms of the volume required for the treatment rather than only in terms of its absorption.

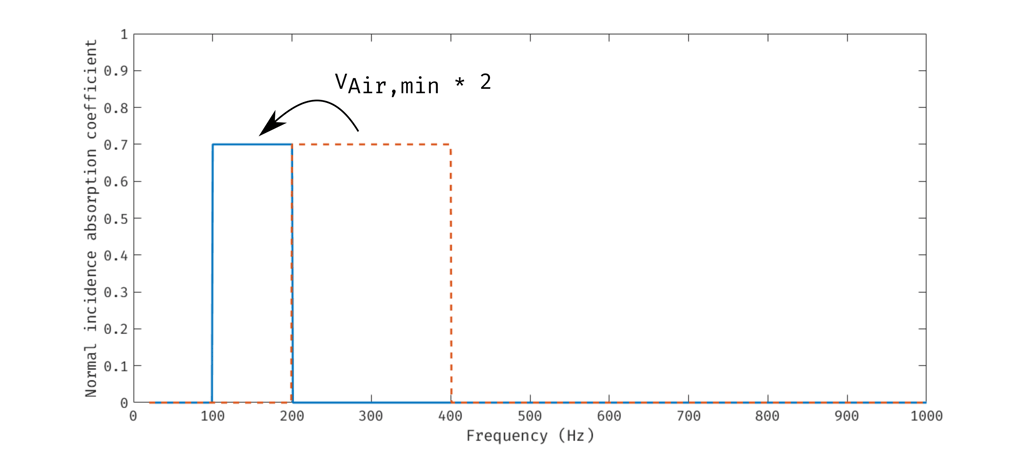
Minimum height

The transverse section of the treatment is the surface of the treatment exposed to the incident wave. For example, in an impedance tube, it corresponds to the cross-section of the tube, regardless of whether the tested sample has a section identical to, smaller than, or larger than that of the tube.

Thus, the minimum air height of the treatment is given by Eq. 2:

C. Evaluation of absorption concentration over the desired frequency range

The treatments studied in the literature are often optimized to maximize their absorption over a frequency range [fmin; fmax] that varies from one article to another. As a result, optimized treatments exhibit a plateau of absorption over the frequency range of interest.

It is possible to evaluate their performance by focusing solely on absorption between fmin and fmax. Indeed, since this is the frequency range used during optimization, it is reasonable to consider that only this part of the spectrum is of interest for application purposes.

This evaluation focuses on the concentration of absorption over the frequency range of interest. In other words, the best evaluation is obtained when the absorption is a step bounded by fmin and fmax.

The performance index (P2) is defined as the theoretical air height required to achieve the absorption of the treatment over [fmin; fmax] relative to the theoretical air height required to achieve complete absorption of the treatment:

Analysis of the performance of an acoustic treatment

When a (meta)material is studied, developed, or optimized, the discussion often revolves around acoustic performance and performance evaluation: is one material better than another? The underlying question is twofold:

• Is the typology of the treatment (types and arrangement of resonances) inherently more favorable than another for effective sound absorption?

• Has the optimization been effective, i.e., has it maximized absorption while minimizing the treatment volume?

A. Evaluation of raw applicative performance

The evaluation consists in comparing the absorption of the treatment to a target absorption: average absorption over a given frequency range, a single-number rating from a standard, etc.

It is therefore essential to compare only treatments optimized with respect to the same objective and of equal thickness. For example, a treatment optimized to maximize absorption over the range [2000; 8000] Hz is expected to show lower average absorption over the range [500; 2000] Hz than another treatment optimized over [500; 2000] Hz. This difference is not due to the typology of the treatments or the quality of their optimization, but to the difference in objective.

A performance index based on such a comparison is necessarily arbitrary, as it is not grounded in a theoretical optimum or a reference standard.

To define the following performance indices, it is necessary to introduce a new quantity that generalizes Eq. 2: the theoretical minimum air height required to achieve a given absorption coefficient over the frequency range [a; b]. In other words, the absorption coefficient is considered zero outside [a; b]:

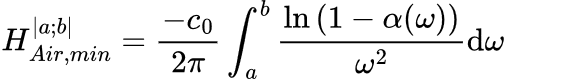
B. Evaluation of the proper use of volume

The evaluation consists of comparing the minimum theoretical volume (or height) of air giving rise to the absorption of the treatment with the volume (or height) of the treatment.

This evaluation focuses solely on the proper use of volume, regardless of whether the absorption coefficient has strong application potential or not. It is a measure of “lost” volumes: solid walls (which cannot be completely eliminated), and above all, the quality of the optimization. Indeed, as presented above, the same absorption can be obtained with different volume treatments.

The performance index (P1) is thus defined as the theoretical height of air required to achieve the absorption of the treatment relative to the height of the treatment:

Example

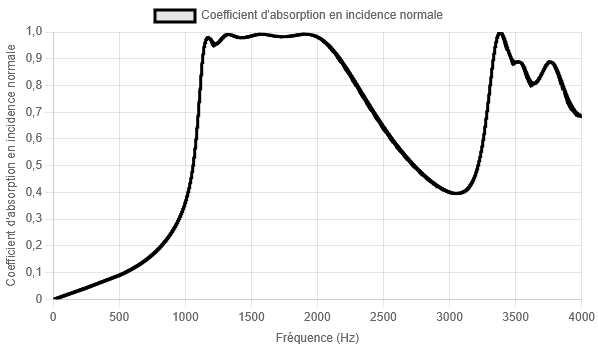
A treatment with a thickness H = 3 cm has an absorption greater than 0.95 in the range [1150; 2100] Hz. Below and above this frequency range, its absorption decreases rapidly and is therefore of no practical interest. It has been optimized to maximize its absorption over [1150; 2000] Hz.

The classic description of the treatment's performance is:

• Sub-wavelength absorption: λₒ(1150 Hz) / H = 9.9... ...

• over 0.9 octave = log2(2100/1150). ...

• and near-perfect > 0.95.

The proposed indices are:

(P1) = 0.79 ➝ The treatment volume is well utilized, with little space lost to structural walls or unnecessarily large resonators. ➝ This type of treatment makes good use of space to generate absorption.

(P2) [1150; 2000] Hz = 0.55 ➝ Absorption is moderately concentrated in the frequency range of interest. In fact, absorption decreases relatively slowly before and after (less problematic) the plateau.